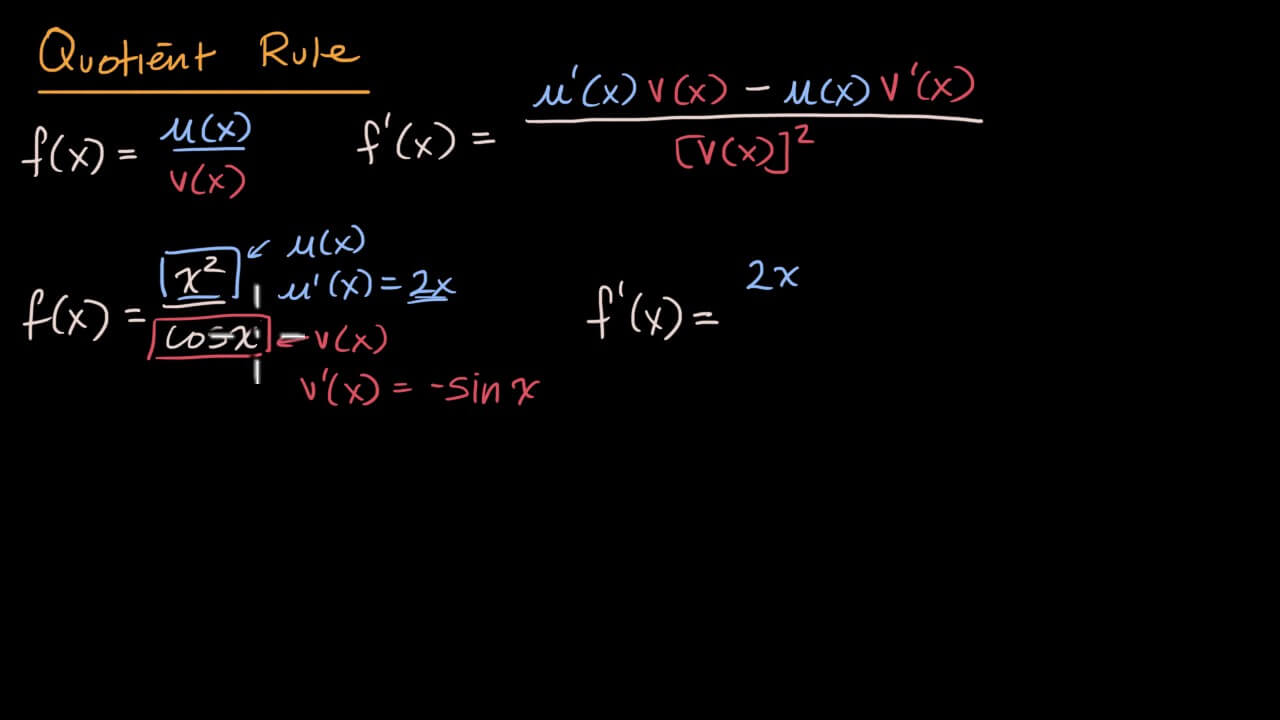Introduction to Quotient Rule with example
While using differentiation, two functions connected by different operators can be differentiated keeping in mind the different operators used. For example, a positive operator is used within two functions. Both the functions can be easily differentiated using the positive operator. The same thing happens with a negative operator as well. But it is not possible in the case of multiplication and division. For multiplication, each of the functions is differentiated separately while keeping the other function constant. But, in the case of division, the process gets more complicated. In this article, we would check out what the quotient rule in differentiation is all about.
Introduction to Quotient Rule
Let us assume that there are two functions f(x) and g(x). Here the functions are differentiable, which means the derivative of both the functions prevails. Thus using the quotient rule, we can find the quotient of the given functions. According to the quotient rule, the derivative of the complete function is the derivative of the numerator times the denominator minus the derivative of the denominator times the numerator which is totally divided using the square of the denominator. Moreover, the quotient rule is quite similar to the product rule, just that we would put negative instead of positive sign. Another important thing is to keep in mind that we need to square the denominator. The formula looks as follows:
H’(x) = d/dxf(x)/g(x) = [f’(x)g(x) – f(x)g’(x)]/[g(x)]2
Let us find whether the function is true or not.
H(x) = f(x)/g(x) {given}
Thus, using product rule, we get,
f’(x) = H’(x)g(x) + g’(x)H(x)
By putting the value of H(x),
f’(x) = H’(x)g(x) + g’(x)f(x)/g(x)
H’(x) = [f’(x) – g’(x)f(x)/g(x)]/g(x)
H’(x) = [f’(x)g(x) – g’(x)f(x)]/[g(x)]2 (Thus Proved)
Example of Quotient Rule
Let us find out the quotient rule utilizing an example. We need to differentiate y=cos x / x2.
So, we can take u = cos x and v = x2
Therefore, the derivative of these two functions would be:
du / dx = – sin x and dv / dx = 2x.
Thus using the formula, we can write:
dy / dx = [v (du / dx) – u (dv / dx)] / [v2]
Thus by putting the values, we get:
dy / dx = [x2 * (- sin x) – cos x * 2 x] / [x2]2
So, by taking out the common factor ( – x) from the above equation, we get:
dy / dx = [ – x( x sin x + 2 cos x)] / x4
dy / dx = [ – ( x sin x + 2 cos x)] / x3
Thus this is the required derivative that we need to find out.
Conclusion
From the above equation, we now know what a quotient rule is regarding the concept of calculus. It is a bit different from the product rule but more or less the formula to find the derivatives. Sometimes by working around with the quotient rule, individuals simply use the complete function to apply within the formula. This is not at all perfect. Firstly, we need to simplify the function, and then move forward with the application process. By utilizing simplification, the function becomes easy to understand and becomes simple and clear to derive.
Cuemath has been helping students with their math lessons online. There are finer concepts regarding calculus, trigonometry, algebra, etc., which the teachers at Cuemath are eager to help students with. Moreover, there are test samples, and exams are also conducted online to strengthen the root level of each student. Book an online class at Cuemath and aid yourself with a profound knowledge of the subject. Cuemath classes are always there to provide help to students regarding different fields of mathematics.